Recursion vs Iteration: What's the difference?

Iteration and recursion similarities and differences

The factorial of 5 is 120.
The factorial of 10 is 3,628,800.

Programmers can take one of two approaches when it comes to the Java factorial problem. They can take an iterative approach, or they can write a program that does Java factorial recursion.

For those who aren’t math wizards, the factorial of a number is the product of all the whole numbers that precede it multiplied together. The number itself is also included in the multiplication. So, 10 factorial (also written as 10!) is:

1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 3,628,800.

Five factorial (or 5!) is:

1 x 2 x 3 x 4 x 5 = 120.

Since these calculations use every integer in a series of numbers, factorial programs lend themselves well to Java training exercises, as they nicely demonstrate loops and iterative structures. They also provide an opportunity to contrast iterative and recursive Java algorithms.

Iterative Java factorial functions

Let’s tackle the iterative approach first. Here’s an iterative Java factorial program that calculates ten factorial:

package com.mcnz.recursion;/* Calculate a factorial without recursion in Java. */public class IterativeJavaFactorialProgram {   public static void main(String[] args) {    int factorialProduct = 1;     for(int i=1; i<=5; i++) {      factorialProduct = factorialProduct * i;      System.out.print(i);    }   System.out.println(“\n Iterative Java factorial result: ” + factorialProduct);  }} /*Output from iterative Java factorial code:1234 Iterative Java factorial result:*/

Recursive Java factorial code

Let’s contrast the iterative approach with a Java program that finds factorials with recursion.

package com.mcnz.recursion; public class RecursiveJavaFactorialProgram {   public static void main(String args[]) {    /* Recursive Java factorial function. */    long nFactoriral = factorialFunction(5);    System.out.println(nFactoriral);  }   /* Java factorial recursive method. */  public static long factorialFunction(long n) {    if (n <= 1) {      return 1;    } else {      return n * factorialFunction(n – 1);    }  }}

Java factorial recursion explained

Notice how the recursive Java factorial function does not need an iterative loop. Instead, the code repeatedly calls itself until a stop condition is met. In this case, the condition to terminate the Java factorial recursion is when the number passed into the factorialFunction method is less than or equal to one.

Many junior developers like the recursive approach to problem solving. Others find this approach difficult to conceptualize.

The recursive Java factorial function stacks method calls on top of each other.

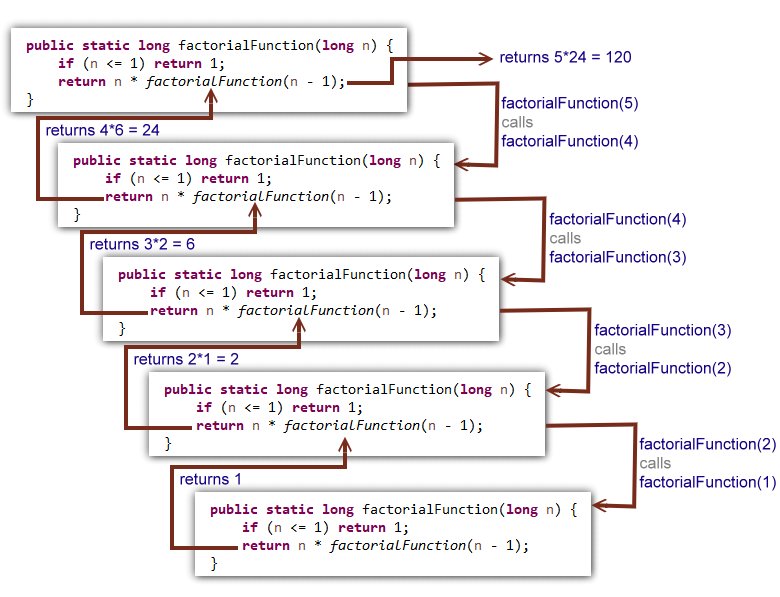
When the recursive Java factorial program runs, it creates a stack of method calls that look like this:

factorialFunction(5)

factorialFunction(4)

factorialFunction(3)

factorialFunction(2)

factorialFunction(1)

When the condition that marks the end of recursion is met, the stack is then unraveled from the bottom to the top, so factorialFunction(1) is evaluated first, and factorialFunction(5) is evaluated last. The order in which the recursive factorial functions are calculated becomes:

1*2*3*4*5

The result is 120.

Iterative vs recursive factorial functions

Note that with an iterative loop, methods calls are not stacked on top of each other. This eliminates the potential for a StackOverflowError to be thrown when loops are used. In contrast, the possibility of a StackOverflowError looms like the sword of Damocles every time you employ Java recursion. A large number of stack frames can crash the Java virtual machine (JVM).

Furthermore, iterative loops allow for linear processing, which on the JVM, is faster than the exponential processing rates associated with Java recursion. If Java performance is important, you should avoid recursion.

Many platforms optimize recursive function calls, but the JVM is not one of them.